Features: The start of machine Learning

Feature Vectors#

As mentioned before , a feature vector gives us a score when the dot product itself $\phi(x)$ and a weight vector $\bold{w}$ is taken.

$\bold{w}$ is found through optimization while $\phi (x)$ is determined based on domain knowledge.

Take determining whether a string is a website or not.

How would we go about it?

Perhaps we know that websites often ends with "com".

But it could just as easily end with "org".

How do we decide which to include and which to not?

That’s where feature template come into play.

Feature templates#

Feature templates is a way in which we can define groups of feature computed in a similar way.

It can be written as using english with blanks (__) denoting places to be filled with arbitrary values.

For example, instead of saying ends with “com” or “org”, we just need to say last three letters are _.

This reduces the burden of the feature engineer and allows them to not need to know specifically what to look at, but rather just know roughly which general pattern direction to look at.

Feature templates are most natural for defining binary features, yes/no, 0/1 features. Of course, non binary features can be used too, such as length of string, pixel intensities etc.

Feature vector representation#

Having defined a framework in which we can define features, we can look at representing them.

A feature template often correspond to many features. The feature template last three letters are _ contains $\large 26^3$ number of features alone.

At the same time, the feature vector corresponding to the feature template are often sparse. The feature vector for last three letters are _ will only ever have 1 of the $26^3$ options selected at any point in time. This representation of state where all but one of the values are 0 is also known as one-hot encoding.

Arrays#

Arrays assume a fixed ordering of features. Each index corresponds to a particular feature.

Often, arrays are used when the feature vector is dense (mostly non zeros). When used correctly, arrays save more space and compute time. Example includes representing the pixel intensity of an image.

Maps#

When it comes to sparse feature vectors however, maps mapping feature name (String) to feature value (float) are more common. Features not in the map are automatically assigned 0.

Defining our feature vector for last three letters are _ feature template:

import collection
feature_vector = collection.defaultdict(float)
feature_vector["last three letters are " + x[-3:]] =  1

Due to the internal structure of maps, there are overheads, and hence much slower when dealing with dense feature vectors.

At the end of the day, regardless of representation method, it is important to be detailed when describing features.

Having a feature template with Num letters equals _: 1 and feature with number of letters: _ is very different.

Hypothesis Class#

The Hypothesis class is the set of all possible predictors that we can get by varying $\bold{w}$ for a given $\phi (x)$.

$\mathcal{F} = { f_{\bold{w}}, \bold{w} \in \real^d }$

With hypothesis class, we can re-look at how learning is done.

Learning in the context of Feature extraction#

Before learning and before choosing our features, we have a space where all predictors are possible.

By setting our feature extractor, we define a set $\mathcal{F}$.

Learning is then done to obtain a particular $f \in \mathcal{F}$.

Visually:

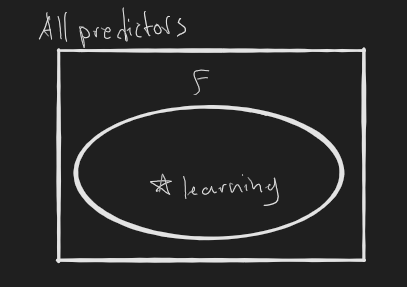
Hence, in some sense, extracting the right features is more important than how we learn.

Why?

Because no amount of learning will make up for a badly defined $\mathcal{F}$ space.

The key then, is to find a way to extract features which can appropriately capture predictors which are good.

Expressivity in Linear Predictors (Still not clear)#

• TODO: Figure out what this Expressivity in linear predictors means

Despite its name, it is possible to have non linear 2d boundaries with linear predictors.

The main thing for a linear predictor is its score and that is linearly related to $\bold{w}$ and $\phi (x)$. The linear predictor itself, however, is not linear in anything (except for linear regression).

Having the score vary linearly with respect to $\bold{w}$ and $\phi (x)$ allows for efficient optimization as it leads to convex optimization problem.

What does it mean for $\bold{w}$ to vary linearly when we are talking about higher dimensions? When I say $\bold{w}$ increases, what does it mean? Does the $w_i$ increases? Or does everything increase? Same question applies to $\phi(x)$. If $\phi(x)$ has a non-linear function, wouldn’t the value of $\phi(x)$ vary non-linearly?

Therefore, it is possible to define arbitrary features that yield non-linear functions.

Doing so will result in linear predictors with non linear 2d boundaries.

I am still confused because $f_{\bold{w}}(x) = \bold{w} \cdot \phi(x)$ (linear regressor, varies linearly, makes sense) and $f_{\bold{w}}(x) = sign(\bold{w} \cdot \phi(x))$ (classifiers). In which case, it stands to reason that since $\bold{w} \cdot \phi(x)$ is linear, should $f_{\bold{w}}$ vary linearly too?